When do we lose correlations under partial Markovian evolution?

Eric P. Hanson

March 21, 2019

Strategy

  • Classical analog: what kind of correlations are we talking about? How can we lose them?

  • What is entanglement?

  • (Briefly:) What quantum evolutions cause a complete loss of entanglement in finite time?

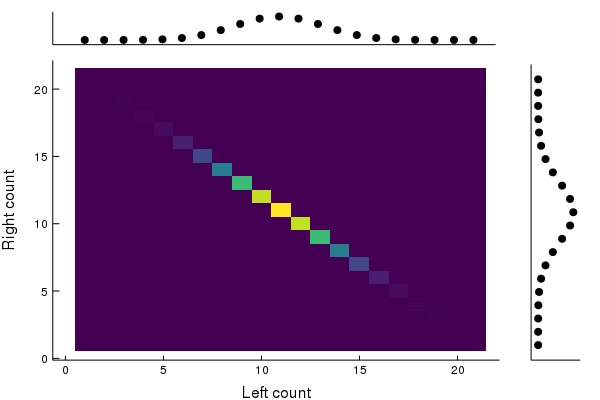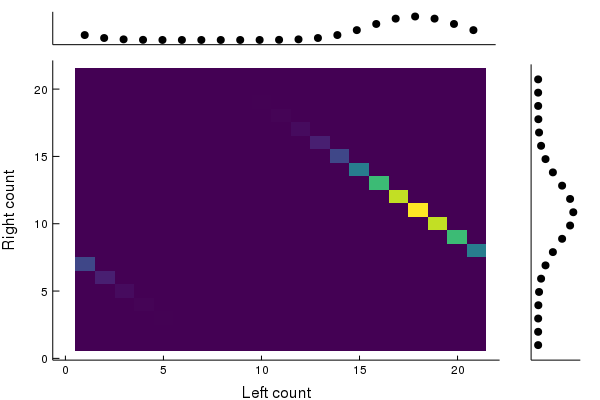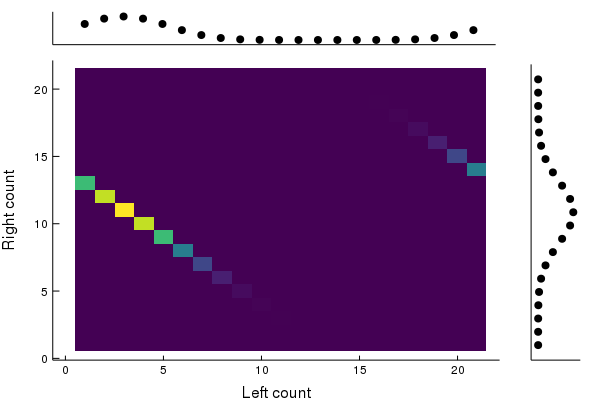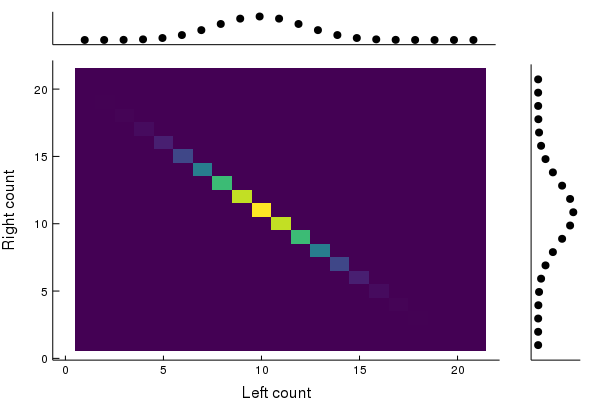
Ehrenfest model (classical)

At each time step, exactly one ball switches sides.

Coupled system

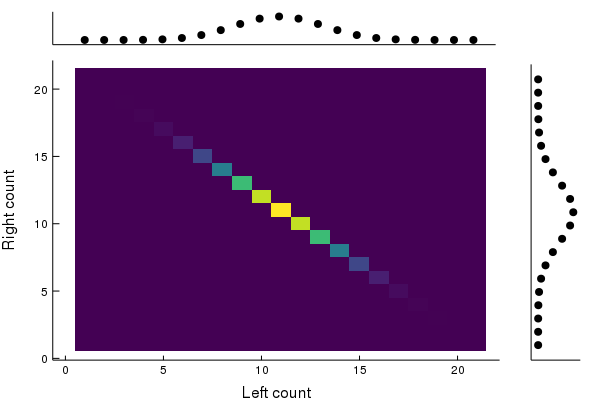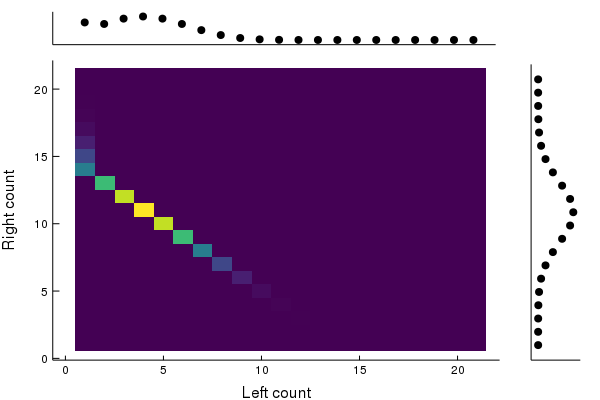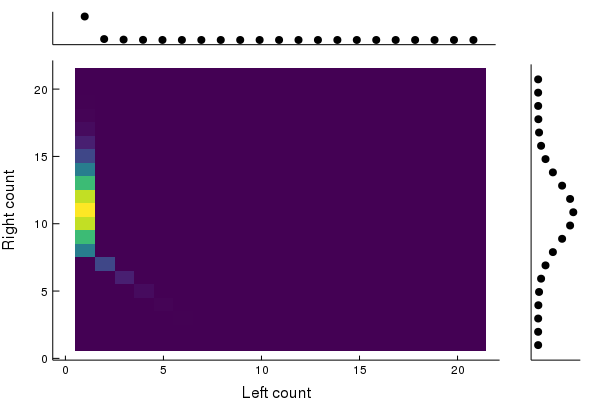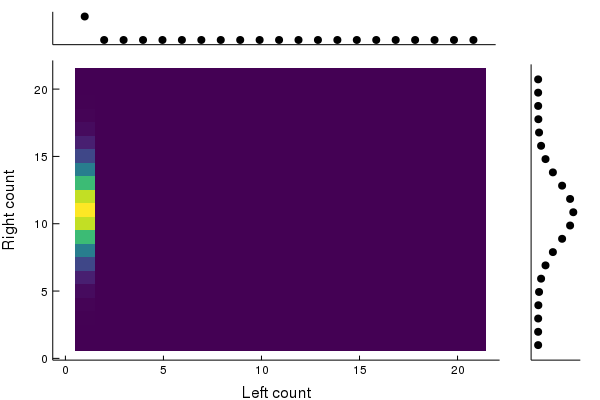
Well-known invariant distribution: π=12N∑n=0N(Nn)(δn⊗δN−n)\pi = \frac{1}{2^N}\sum_{n=0}^N{N \choose n} (\delta _n \otimes \delta _{N-n})

Perfectly correlated!

Loss to the environment

Loss of correlations! Becomes δ0⊗p\delta _0 \otimes p for p=12N∑n=0N(Nn)δN−np = \frac{1}{2^N}\sum_{n=0}^N{N \choose n} \delta _{N-n}.

Loss to the environment

Loss of correlations! Becomes δ0⊗p\delta _0 \otimes p for p=12N∑n=0N(Nn)δN−np = \frac{1}{2^N}\sum_{n=0}^N{N \choose n} \delta _{N-n}.

Alternate dynamics: Birth-death

At each timestep, prob. 110\frac{1}{10} for a ball to be born (until 20); prob. 110\frac{1}{10} for ball to die (until 0). Otherwise nothing happens.

Alternate dynamics: Birth-death

10 timesteps per frame, 600 total timesteps.

Loss of correlations! Asymptotically converges to u⊗pu \otimes p for uu uniform.

More generally: irreducible + aperiodic

Initial joint distribution: π=12N∑n=0N(Nn)(δn⊗δN−n)\pi = \frac{1}{2^N}\sum_{n=0}^N{N \choose n} (\delta _n \otimes \delta _{N-n}).

Let PP be irreducible and aperiodic with invariant distribution qq. Then π(Pk⊗id⁡)=12N∑n=0N(Nn)((δnPk)⊗δN−n)→12N∑n=0N(Nn)(q⊗δN−n)=q⊗p\begin{aligned}\relax \pi ( P^k \otimes \operatorname{id}) &= \frac{1}{2^N}\sum_{n=0}^N{N \choose n} ( (\delta _n P^k) \otimes \delta _{N-n}) \\ & \rightarrow \frac{1}{2^N}\sum_{n=0}^N{N \choose n} ( q \otimes \delta _{N-n}) = q \otimes p \end{aligned}
where p=12N∑n=0N(Nn)δN−np = \frac{1}{2^N}\sum_{n=0}^N{N \choose n} \delta _{N-n}. Decouples!

But we don’t always lose correlations!

But we don’t always lose correlations!

Summary of the classical case

If we let one part of a joint system evolve independently, the two may decouple.

That decoupling can take infinitely long

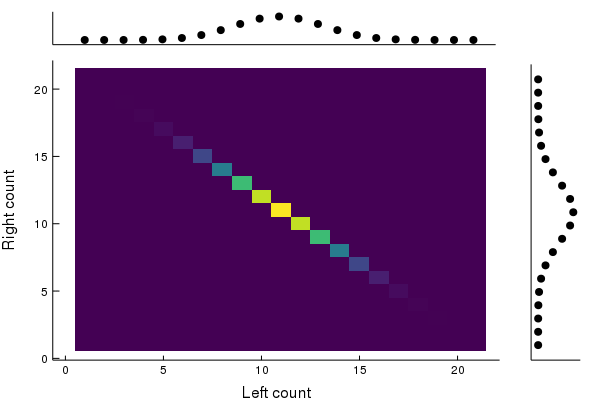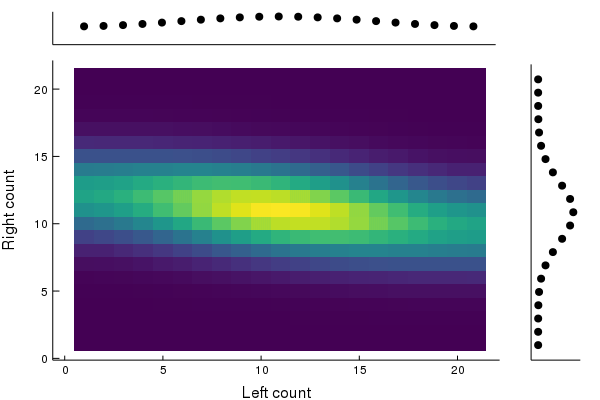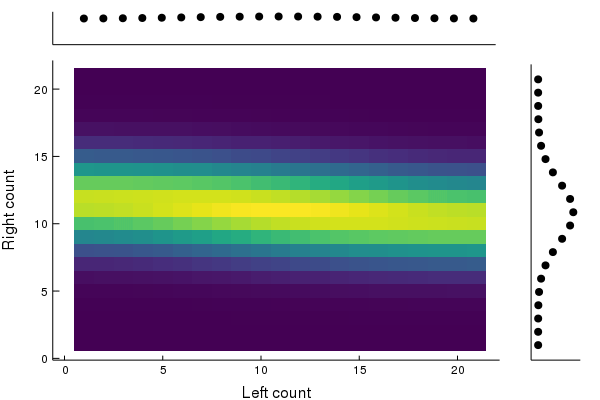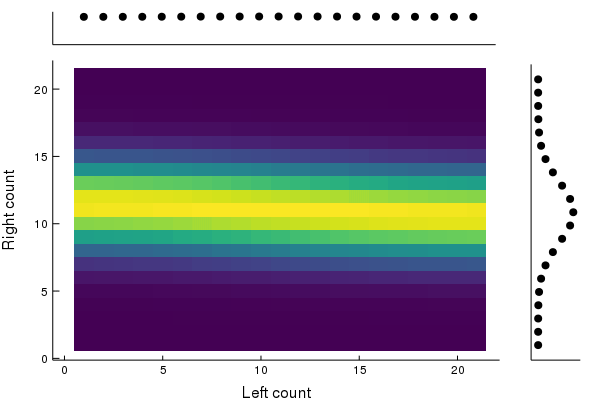
Under periodic evolution, the joint system may not decouple.

Classical →\textcolor{purple}{\to} quantum

  • Probability distributions p∈Rdp \in \mathbb{R}^d →\textcolor{purple}{\to} quantum states ρ∈Md×d\rho \in M_{d\times d}.
    • pi≥0→ρ⪰0p_i \ge 0 \textcolor{purple}{\to}\rho \succeq 0,
    • ∑ipi=1→tr⁡[ρ]=1\sum _i p_i = 1 \textcolor{purple}{\to}\operatorname{tr}[\rho ] = 1.
  • Markov transition matrix PP →\textcolor{purple}{\to} Φ\Phi linear, completely positive, trace-preserving map.
    • PP maps Rd\mathbb{R}^d to Rd\mathbb{R}^d →\textcolor{purple}{\to} Φ\Phi maps Md×dM_{d\times d} to Md×dM_{d\times d}
  • Joint distribution ∑iλipi⊗qi\sum_i \lambda_i p_i \otimes q_i (convex combination of product distribution) →\textcolor{purple}{\to} joint state ρ∈Md×d⊗Md×d\rho \in M_{d\times d} \otimes M_{d\times d}.
    • Key difference: it can be that ρ∈Md×d⊗Md×d\rho \in M_{d\times d} \otimes M_{d\times d} cannot be expressed as ∑iλiρi⊗σi\sum_i \lambda_i \rho _i \otimes \sigma _i for ρi⪰0\rho _i \succeq 0 and σi⪰0\sigma _i \succeq 0, and a probability distribution {λi}\{\lambda_i\}. Entanglement!

Entanglement

Entanglement is a non-classical correlation between the two systems. It is a bit of a strange type of correlation.

  • “No-signalling”; you can’t use entanglement alone to send messages

  • “Superdense coding” One can communicate 2n bits of classical information by only transmitting n bits of data, using n pre-shared “bits of entanglement” (n pairs of entangled qubits)

Which states are entangled?

3D cross section of two-qubit quantum states.

  • Green: all states.

  • Blue: classical states.

  • Inside green, outside blue: entangled states

Avron, Joseph, and Oded Kenneth. 2019. “An Elementary Introduction to the Geometry of Quantum States with a Picture Book.” http://arxiv.org/abs/1901.06688.

What can you do with entanglement?

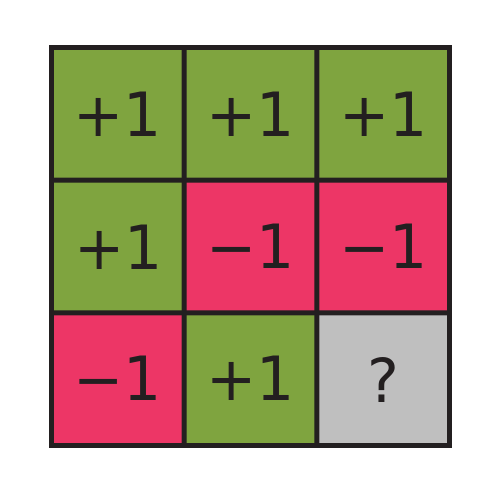
Magic square game

Task: Two isolated, cooperative players Alice and Bob try to construct a magic square

Rows must have an even number of −1-1’s

Columns must have an odd number of −1-1’s

Winning the game

Alice and Bob are judged probabilistically:

  • the referee asks Alice for one specific row, and Bob for one specific column (e.g. top row, second column)

  • Alice’s row must have an even number of −1-1’s, and Bob’s column an odd number, and they must agree on the intersection.

  • That’s it! They win or lose the game.

  • Classically, the best they can do is win 8/98/9 percent of the time

  • If they have access to pre-shared entanglement, they can win every time!

How do we lose quantum entanglement?

Classically…

If we let one part of a joint system evolve independently, the two may decouple.

That decoupling can take infinitely long

Under periodic evolution, the joint system may not decouple.

Irreducible + aperiodic quantum evolutions

  • Similar to property to the classical case: Φn(ρ)→σ\Phi ^n(\rho ) \rightarrow \sigma for any ρ\rho.

  • Just like in the classical case, this gives convergence of the joint state to a product state (here, σ⊗I/d\sigma \otimes I/d where I/dI/d is the identity matrix )

  • It turns out, product states of full support are in the interior of the set of separable states.

  • Then the convergence Φn(ρ)→σ\Phi ^n(\rho ) \rightarrow \sigma gives that there is a finite time for any joint state to become separable under this evolution.

Which evolutions destroy all entanglement in finite time?

  • Irreducible + aperiodic

  • Direct sums thereof

  • Any map such that after some number iterations, it is a direct sum of irreduce + aperiodic maps.

  • That’s it!∗^*

∗*: up to a faithfulness assumption, namely that there exists an invariant state with full support (possibly non-unique).

[Joint work with Cambyse Rouzé and Daniel Stilck França (https://arxiv.org/abs/1902.08173).]