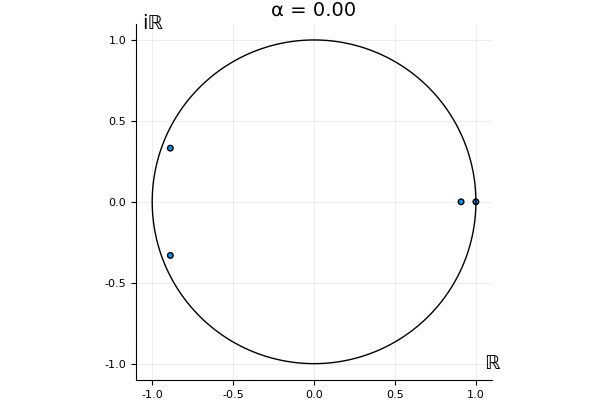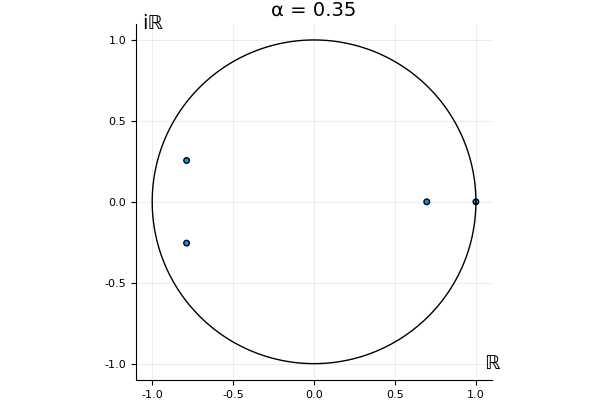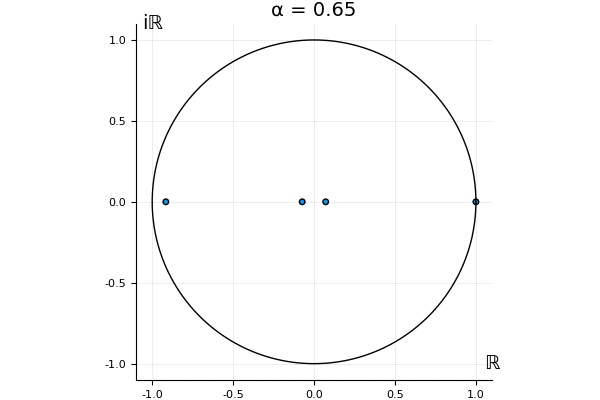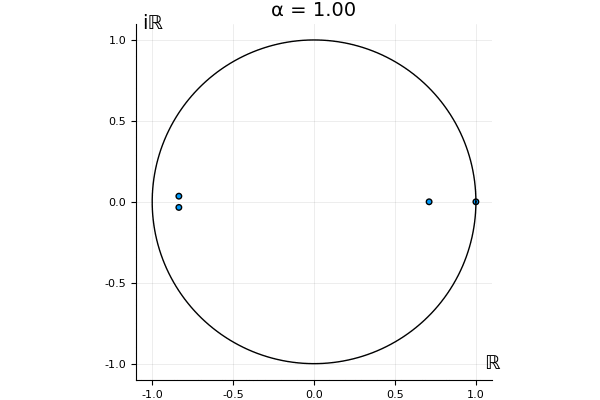
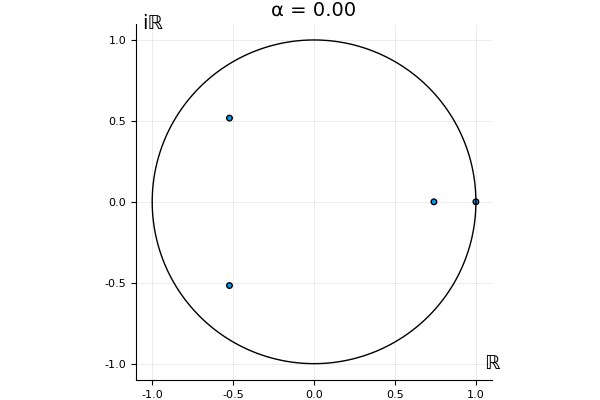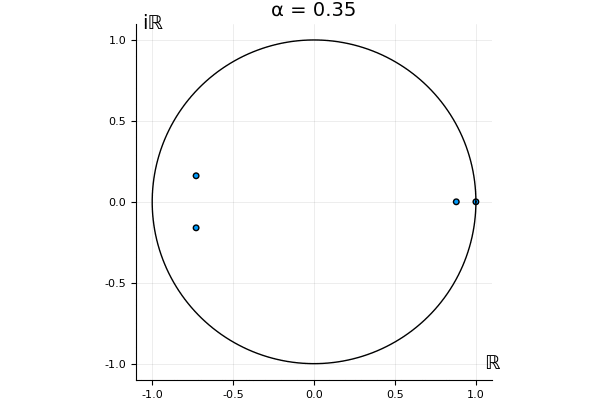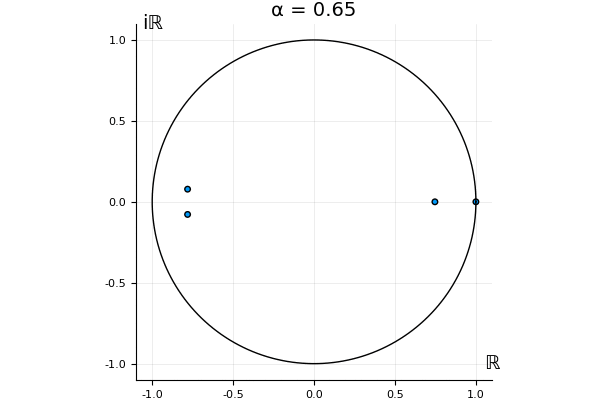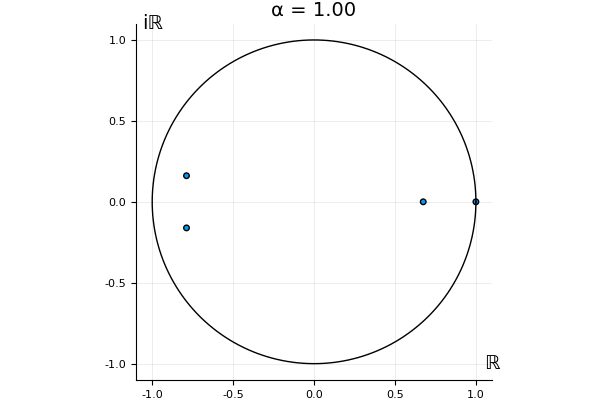
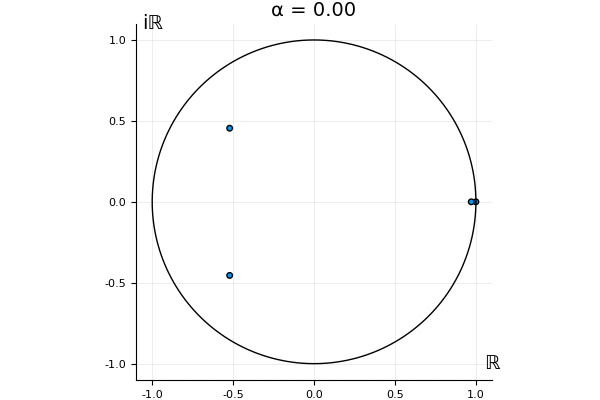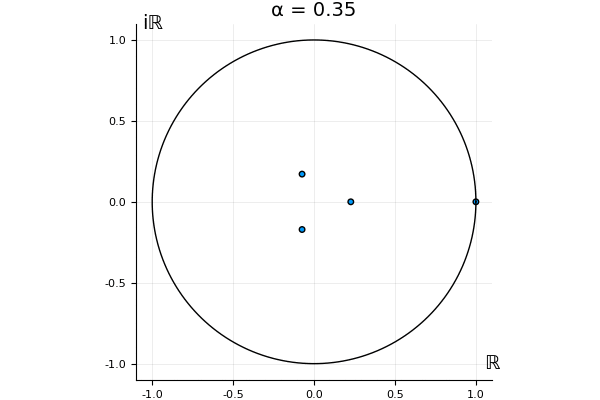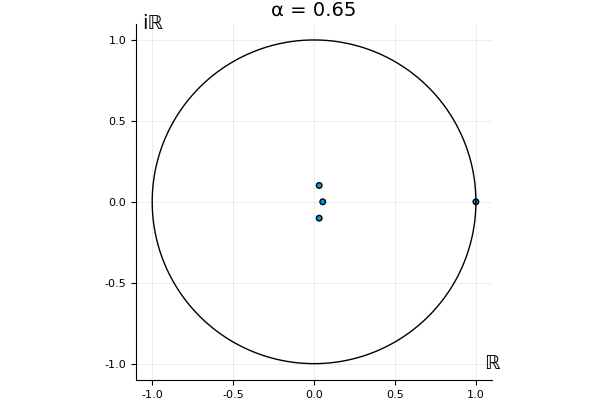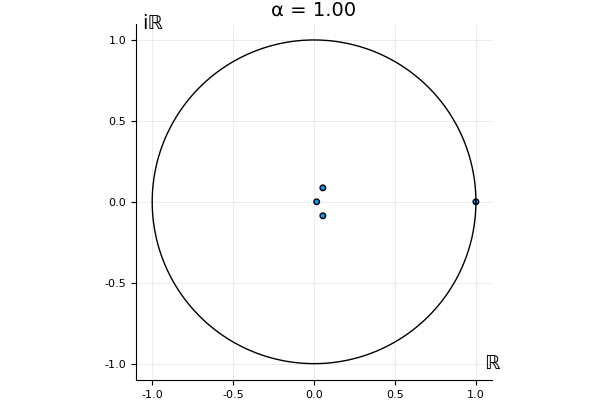
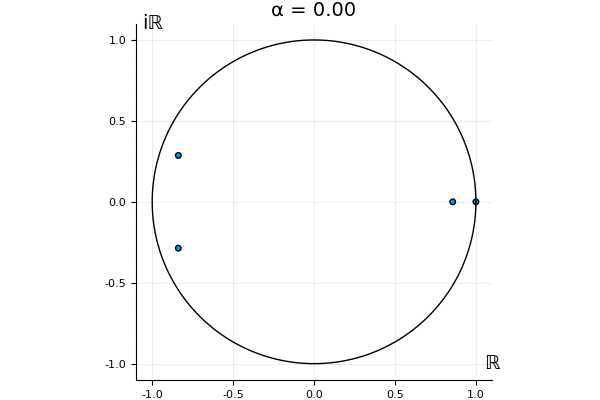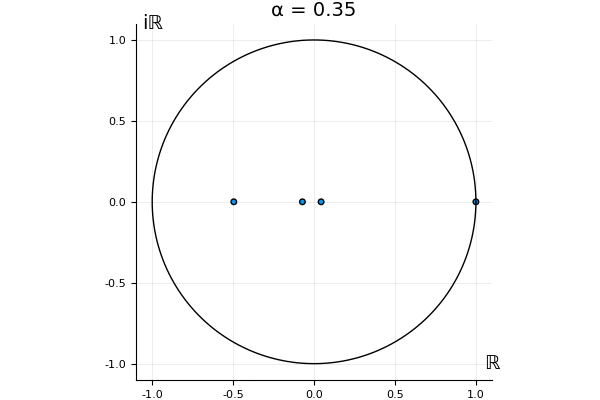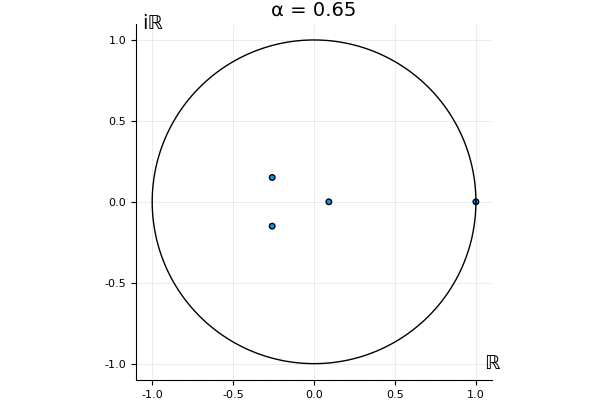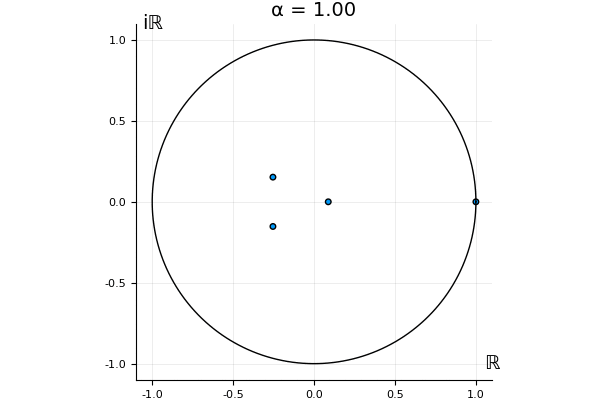
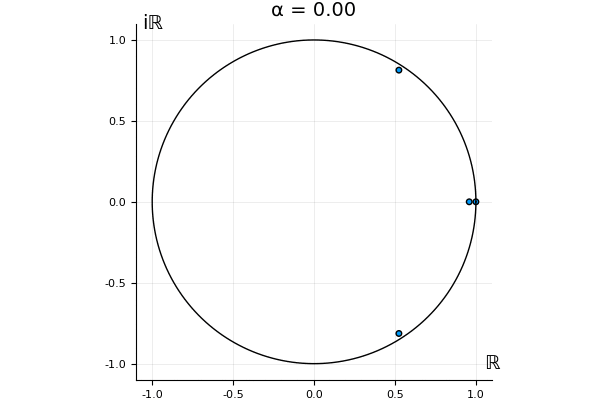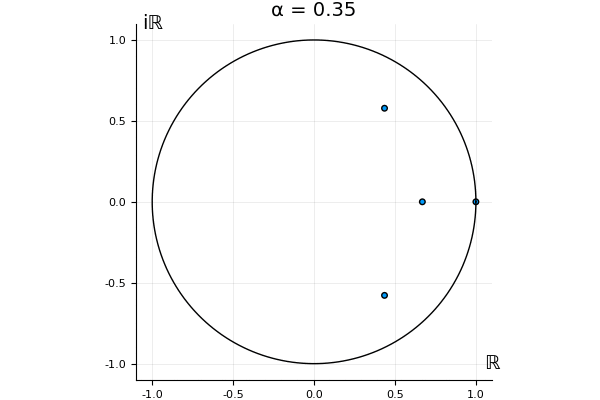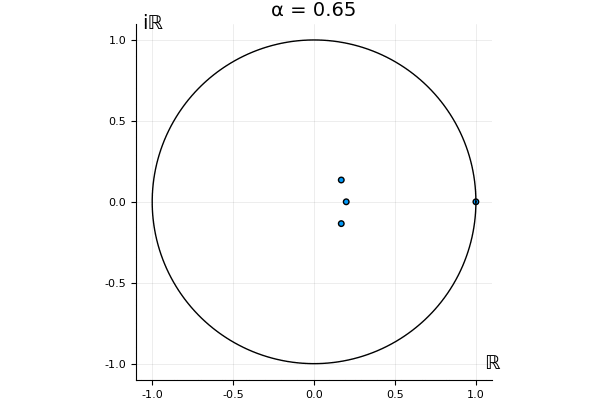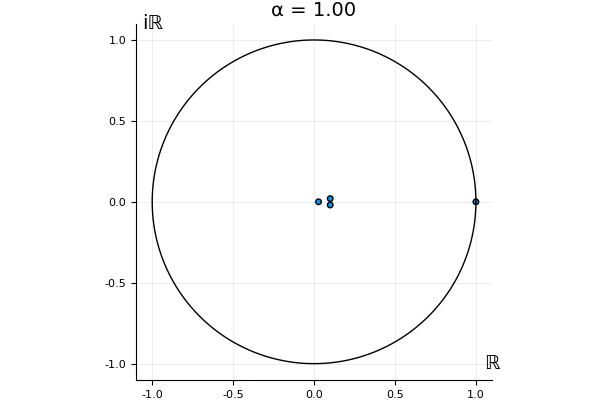
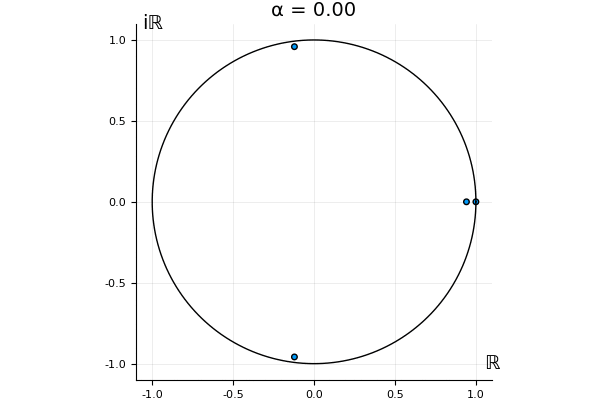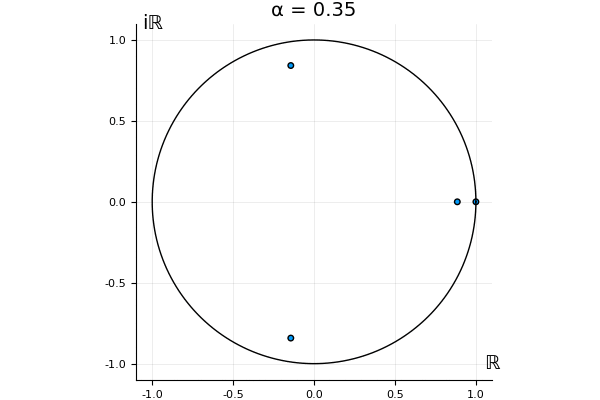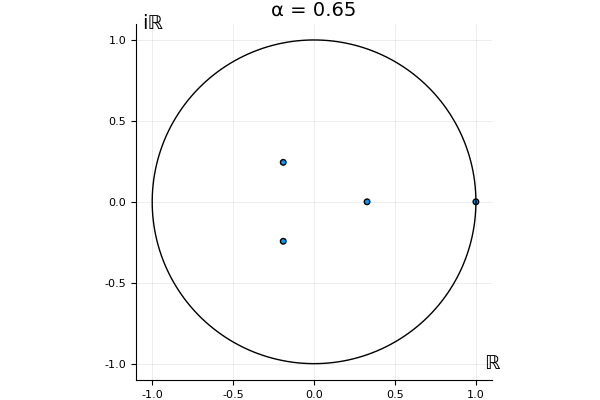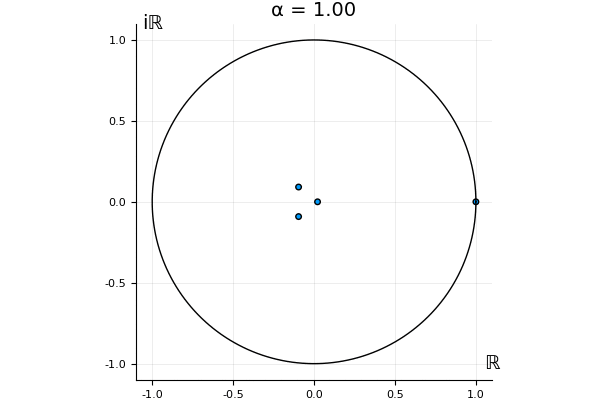
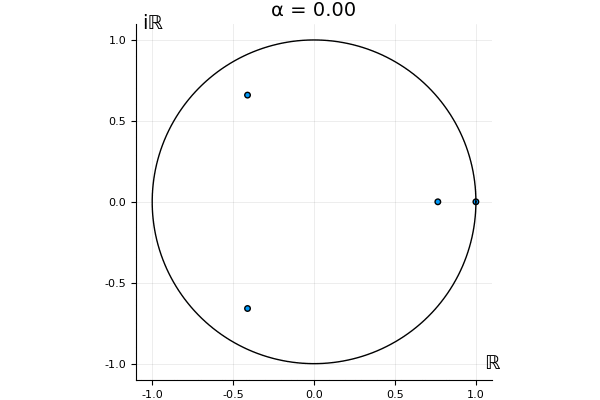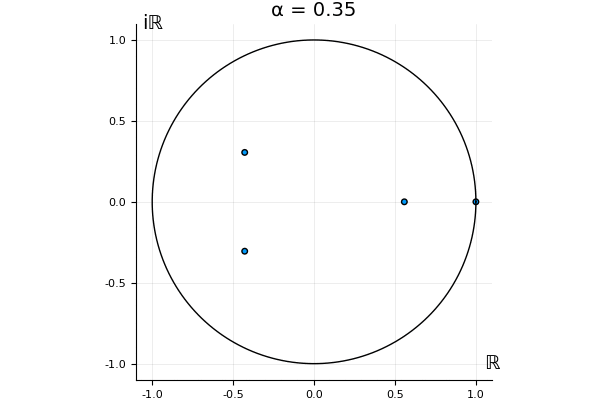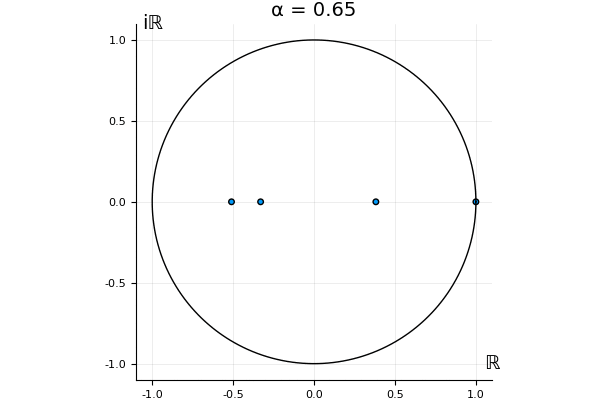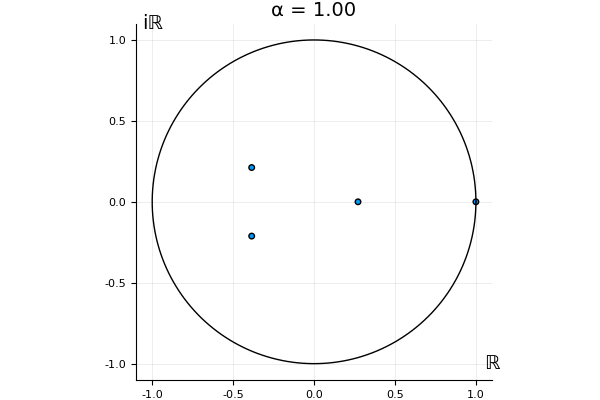
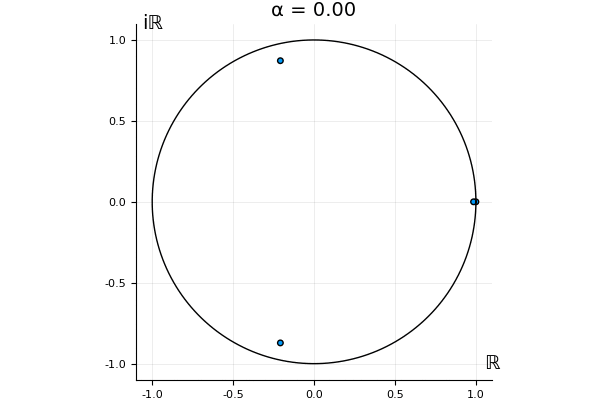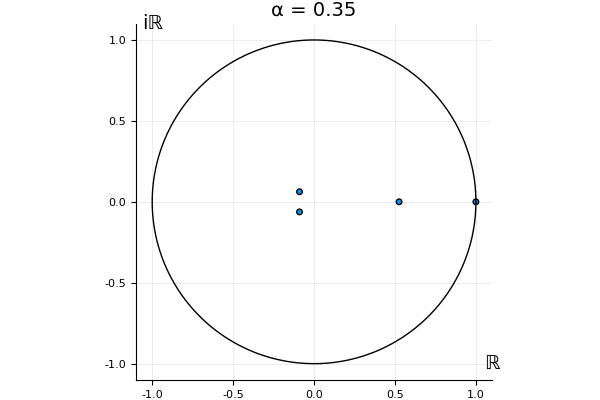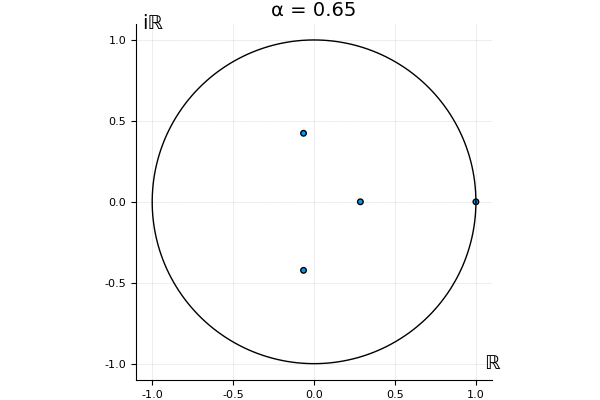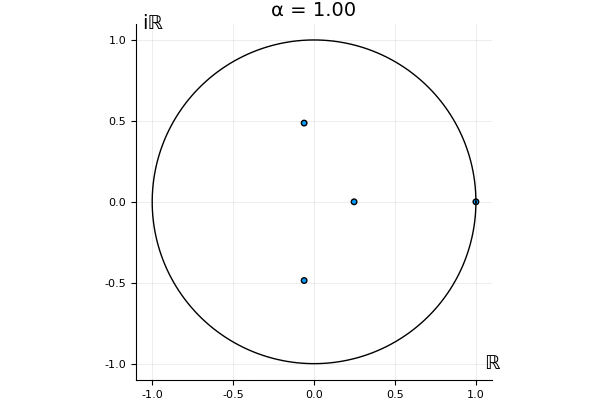
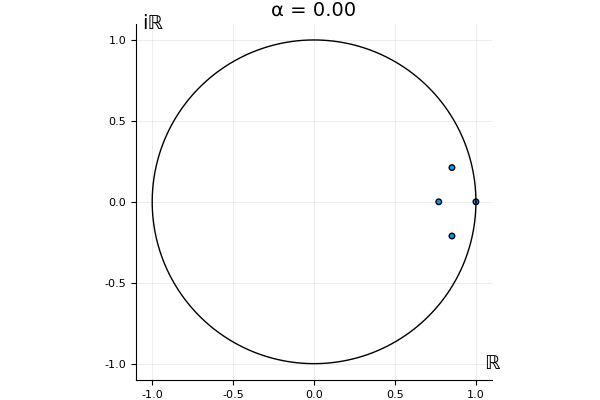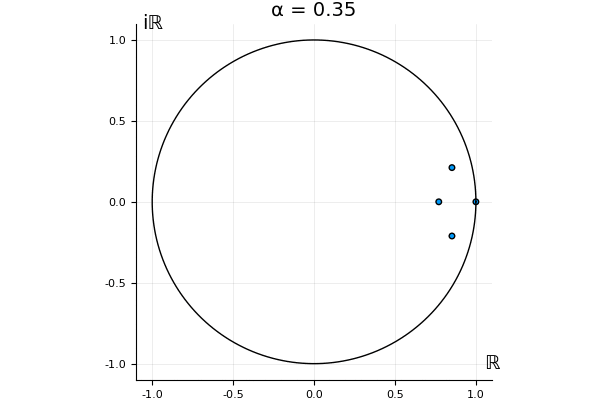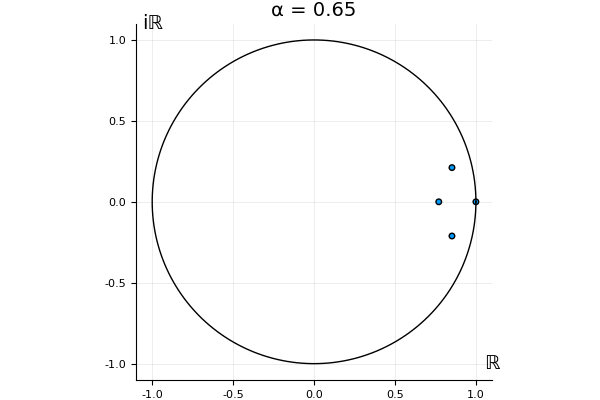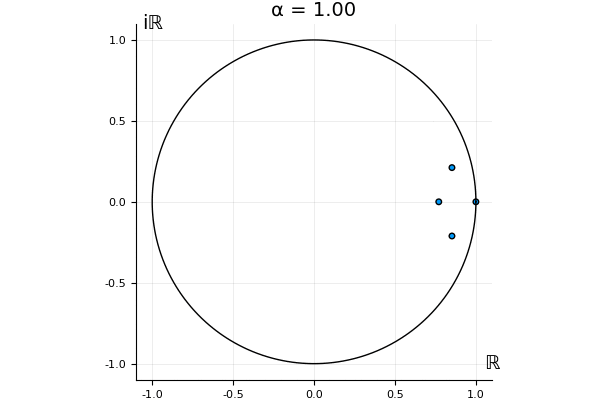
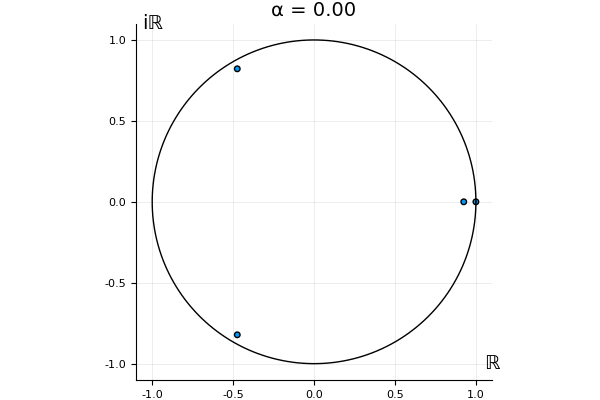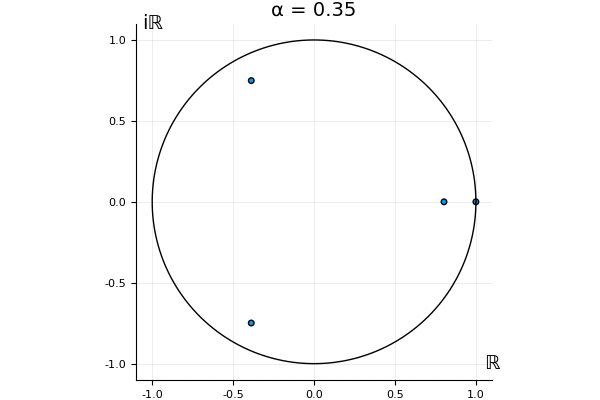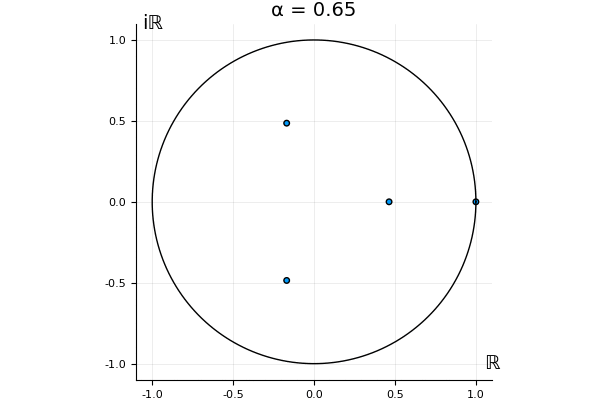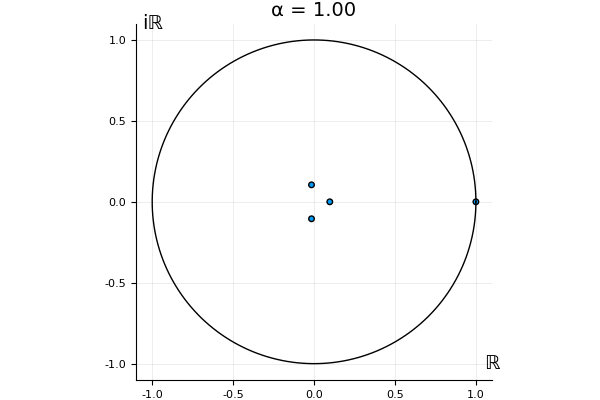
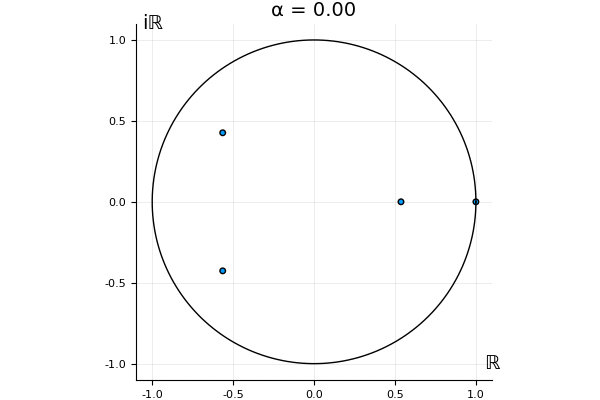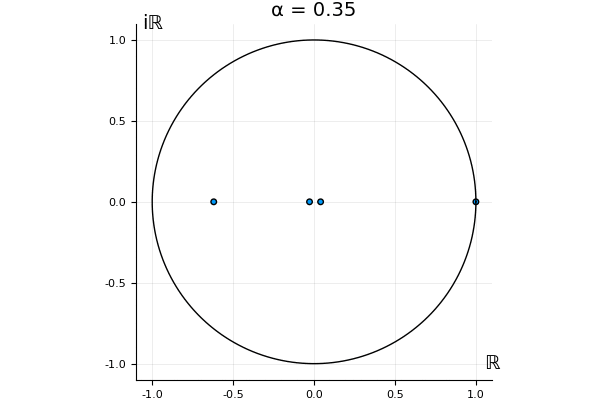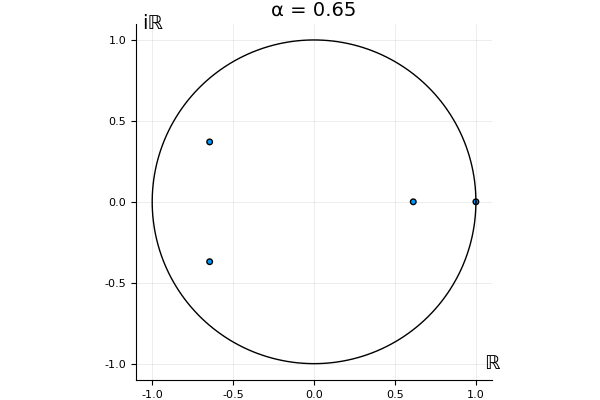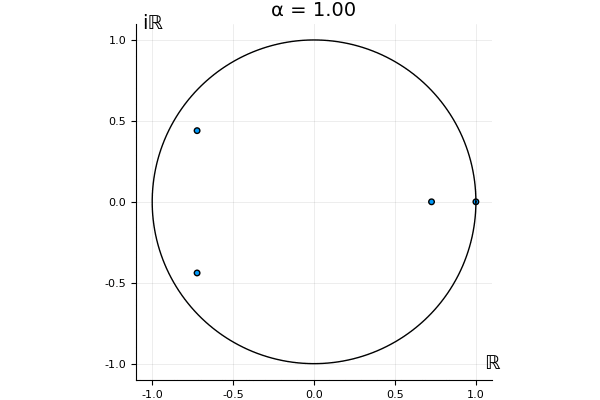
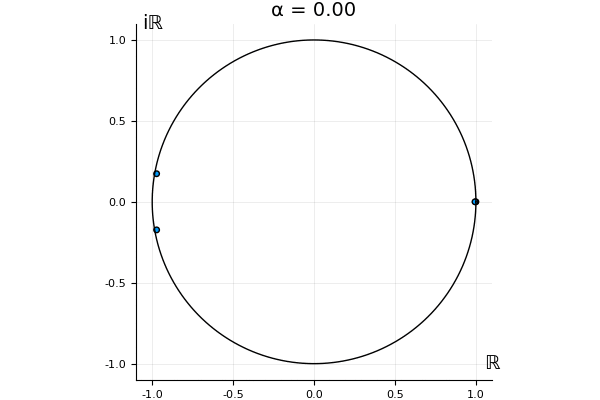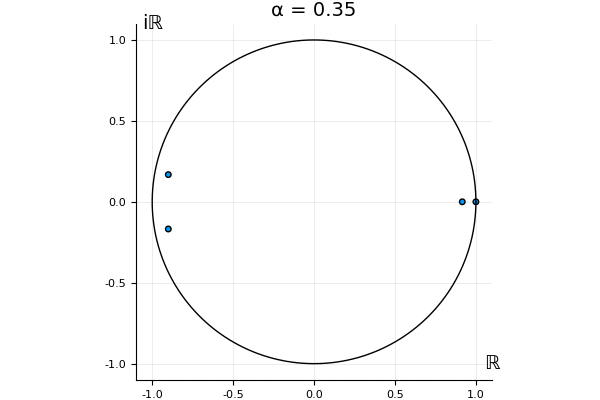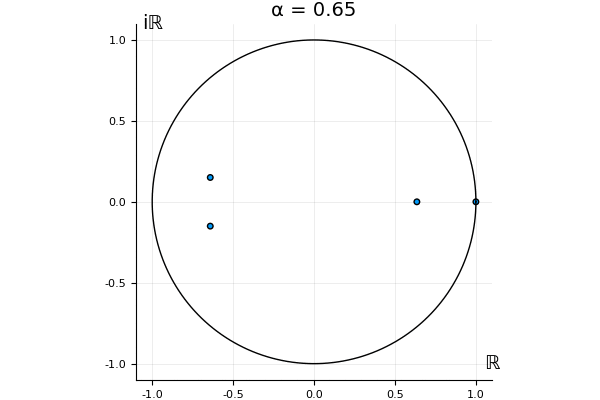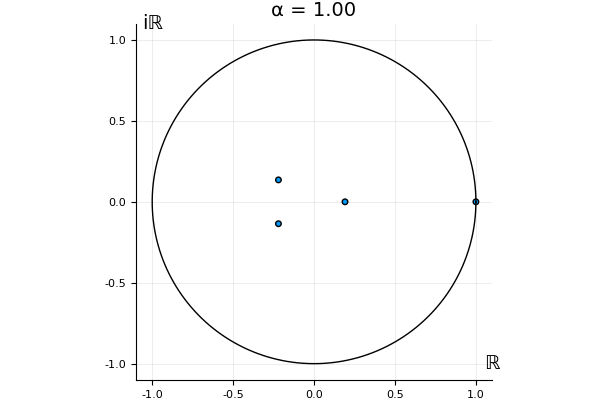
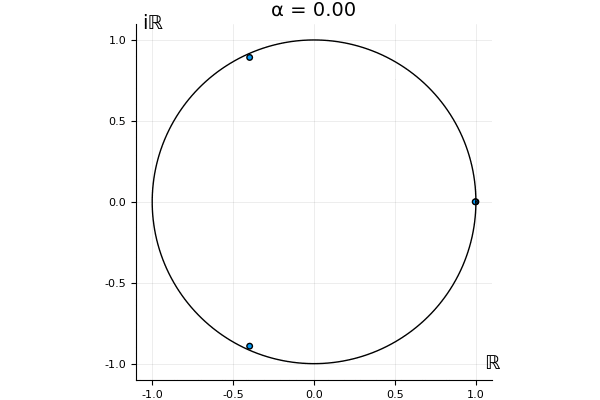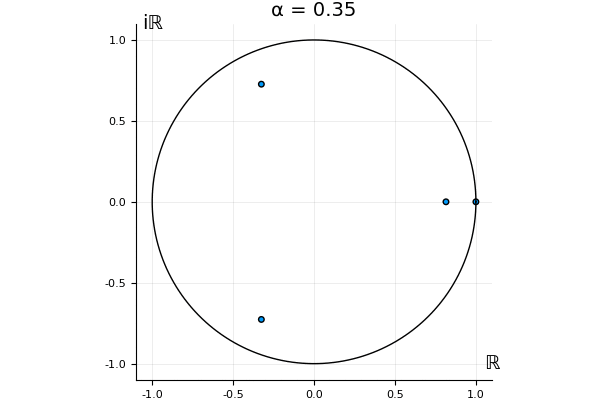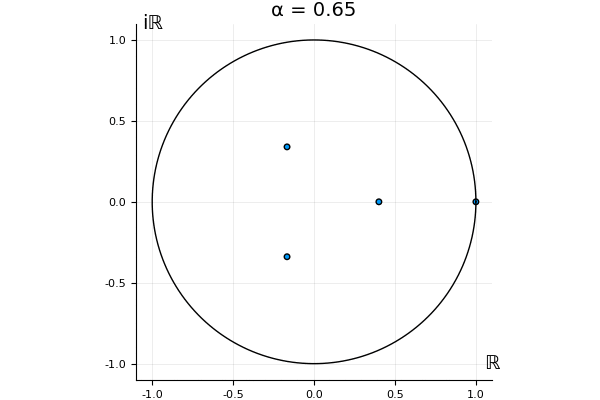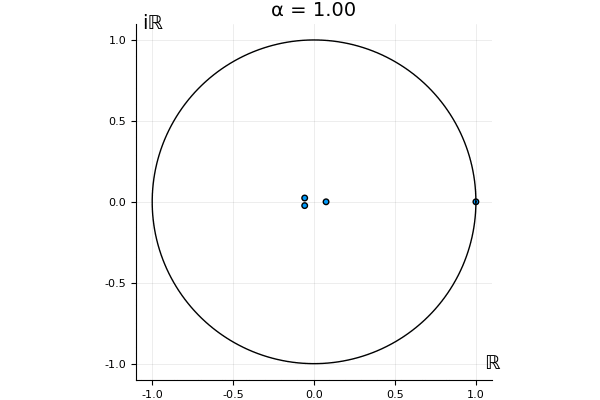
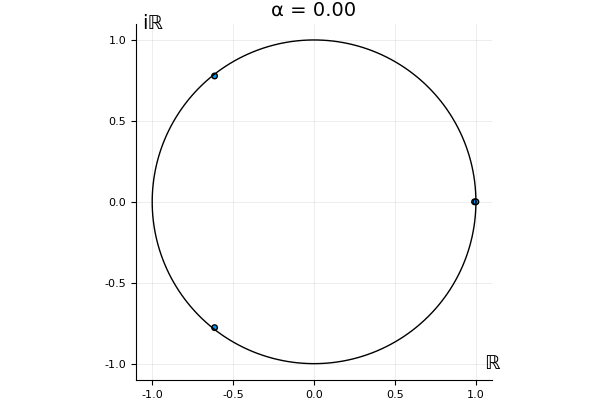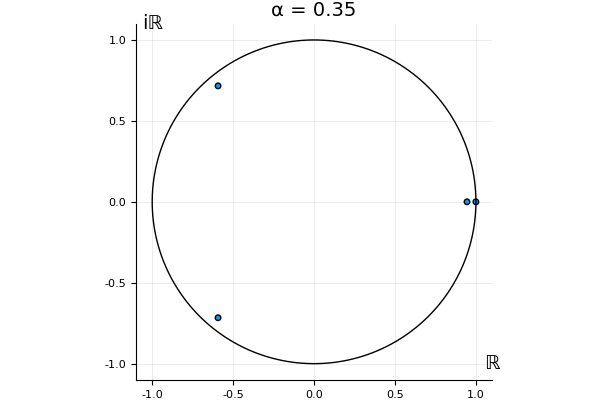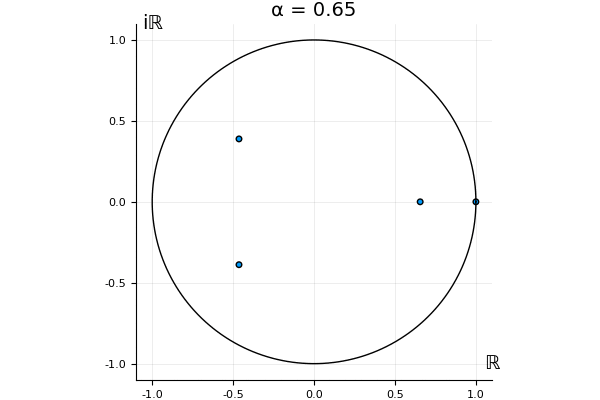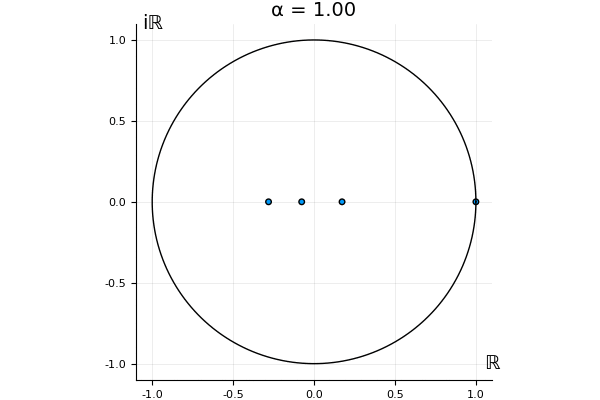
The motivation behind this post is to show some off some nice gifs. But I thought maybe they aren’t actually interesting without any context, so below I’ll try to explain what the gifs are about.
Brief mathematical introduction to Perron-Frobenius theory
Consider the set of \(n\times n\) matrices \(M_n\), with complex entries. The algebraic structure (scalar multiplication by complex numbers, addition and multiplication of matrices) plays well with the operator norm,
\[
\|A\| = \sup_{ v\in \mathbb{C}^n: \|v\|_2=1 } \|A v\|_2
\]
and the involution \(*\) (i.e. conjugate-transpose), making it a C\(^*\)-algebraI recommend p. 17 of Jane Panangaden’s thesis for an excellent diagram explaining the interplay between these structures, along with much more on C\(^*\)-algebras. Panangaden, J. (2016), Energy Full Counting Statistics in Return-to-Equilibrium. McGill University, Montreal QC.
. A matrix \(A\in M_n\) is positive semi-definite if it can be written as \(A= B^*B\) for some other matrix \(B\in M_n\).
Let us now go one level higher: we will consider linear maps \(\phi\) from \(M_n\) to \(M_n\), i.e. linear maps whose arguments are themselves matrices. Such a linear map is positive if it maps positive elements of \(M_n\) to positive elements of \(M_n\). Since \(\phi\) is a linear map on a vector space (even if that vector space is itself the set of matrices), it has eigenvalues and eigenvectors. The eigenvalues are in general complex numbers, and number \[ r = \max\{ |\lambda| : \lambda \text{ is an eigenvalue of }\phi \} \] is the spectral radius of \(\phi\).
With these definitions, we can consider the following Perron-Frobenius type theorem considered by Evans and Høegh-Krohn in 1978Evans, D. E. and Høegh-Krohn, R. (1978), Spectral Properties of Positive Maps on C\(^*\)-Algebras. Journal of the London Mathematical Society, s2-17: 345–355.
:
This may sound abstract (or maybe not), but it is quite nice. A priori, we don’t know that the spectral radius itself is an eigenvalue; from the definition, we only know there is an eigenvalue whose absolute value is the spectral radius. But the above theorem tells us that if \(\phi\) is a positive map, then indeed the spectral radius itself is an eigenvalue, and that the corresponding eigenvector \(A_0\) is positive.
This result is relevant, e.g., for understanding repeated interaction systems. These are discrete-time quantum systems, and the time evolution is given by a positive linear map with spectral radius 1. The quantum states \(\rho\) are given by positive elements of \(M_n\) with trace 1. The above theorem then tells us that there is automatically an invariant state, i.e. a quantum state \(\rho\) such that \(\phi(\rho)=\rho\). Note we are using both that the spectral radius is an eigenvalue (so there is an invariant matrix), and that the corresponding eigenvector is positive (so once we divide by its trace, it is a quantum state).
Let us assume \(A_0\) is invertible. We can define a modified version of the map \(\phi\) by \[ \hat \phi (B) = \frac{1}{r} A_0^{-1/2} \phi(A_0^{1/2} B A_0^{1/2} )A_0^{-1/2} \in M_n \qquad(1)\] for \(B\in M_n\). In fact, this map comes up in the proof of the theorem. Now, with the knowledge of the theorem, we see that this map acts on the identity matrix \(I\) by \[ \hat \phi (I) = \frac{1}{r} A_0^{-1/2} \phi(A_0^{1/2} A_0^{1/2} )A_0^{-1/2} = \frac{1}{r} A_0^{-1/2} (r A_0) A_0^{-1/2} = I \] so in fact, \(\hat \phi\) has the eigenvalue 1 with associated eigenvector \(I\).
A particular deformation
A particular typeThese are the completely positive maps, which are usually defined in a different way, but the usual definition is equivalent to the one I’ll give here.
of positive linear map on \(M_n\) is one which can be represented as
\[
\phi (B) = \sum_{i=1}^{k} V_i^* B V_i
\]
for some \(V_1,\dotsc,V_k \in M_n\). The matrices \(V_i\) are called the Kraus operators. So \(\phi\) acts on \(B\) by conjugating it by each \(V_i\) and adding up the result.
Let us fix such a map \(\phi\), and moreover assume that \(\phi\) has spectral radius 1, with the associated eigenvalue as the identity matrix. By the definition, we see this implies \[ \phi (I) = \sum_{i=1}^{k} V_i^* V_i = I. \]
It turns out when considering the statistics of measurements of a repeated interaction systemin which case, the \(\phi\) of this section is actually the adjoint of the time-evolution operator
, a particular deformation of \(\phi\) becomes important. Let \(v\in \mathbb{R}^k\) be a real vector with strictly positive entries. Then define
\[
\phi^{(\alpha)} (B) = \sum_{i=1}^{k} v_i^\alpha V_i^* B V_i
\]
for \(\alpha\in \mathbb{R}\). Note that \(\phi^{(0)} = \phi\). For real \(\alpha\) this map is still positivein fact, still completely positive, with Kraus operators \(v_i^{\alpha/2} V_i\).
, but no longer has spectral radius 1 or \(\phi^{(\alpha)}(I) = I\), in general. However, by the theorem above, the spectral radius \(r(\alpha)\) is an eigenvalue of \(\phi^{(\alpha)}\), and has a corresponding eigenvector \(A_0(\alpha)\) which is a positive element of \(M_n\). Let us consider the modification of the map given in (eq. 1), defined by
\[
\hat \phi^{(\alpha)} (B) = \frac{1}{r(\alpha)} A_0(\alpha)^{-1/2} \phi^{(\alpha)}(A_0(\alpha)^{1/2} B A_0(\alpha)^{1/2} )A_0(\alpha)^{-1/2} \in M_n
\]
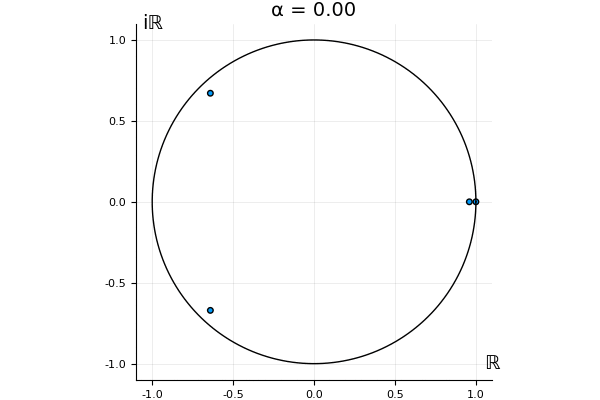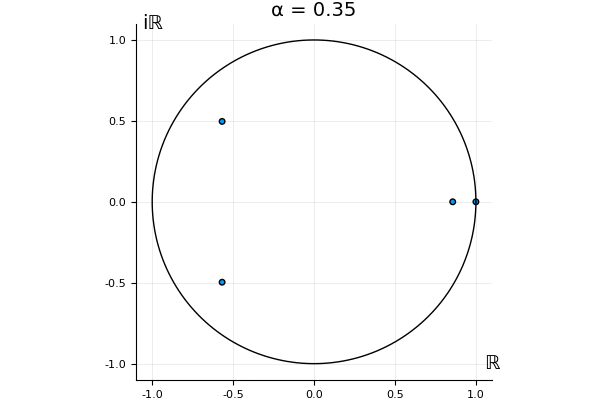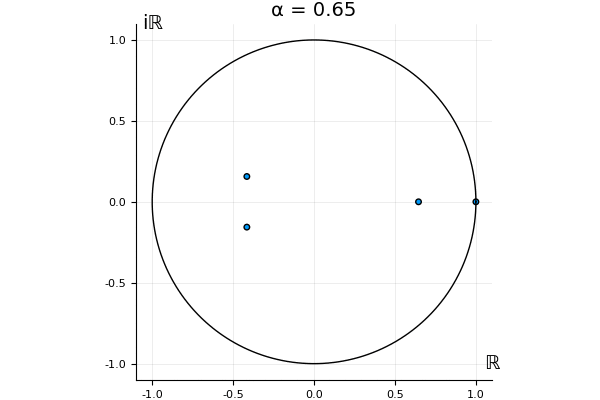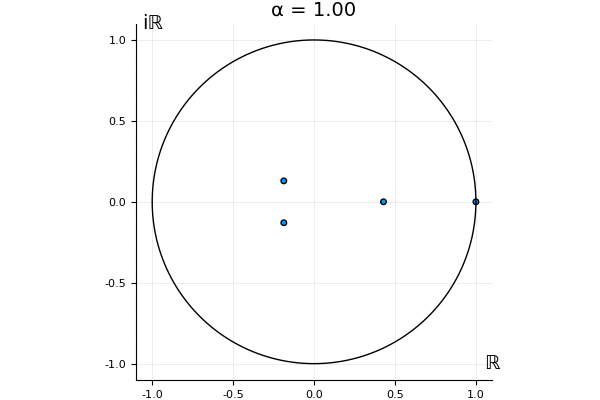
for \(B\in M_n\). Now, we automatically have \(\hat \phi^{(\alpha)} (I) = I\). So the undeformed map, \(\phi\) has this property, and so does \(\hat \phi^{(\alpha)}\). That is, we know what happens to the eigenvalue 1 and the associated eigenvector when we go from \(\phi\) to \(\hat \phi^{(\alpha)}\): they stay the same, for any \(\alpha\).
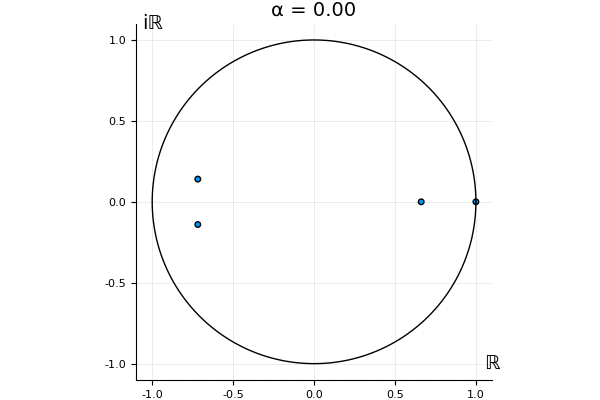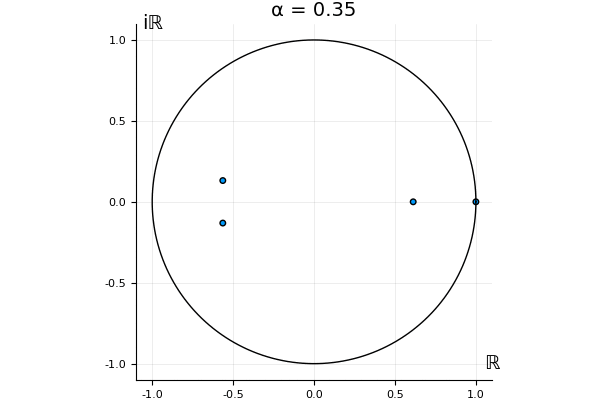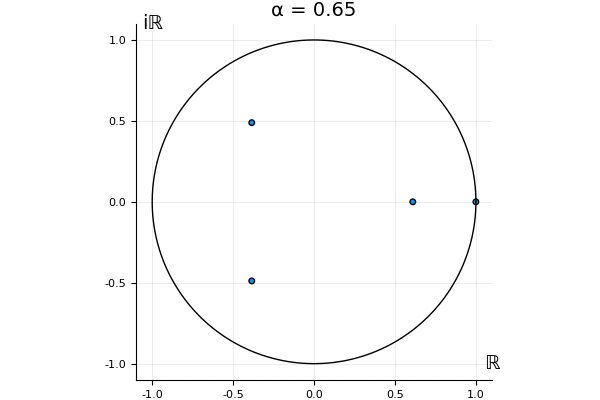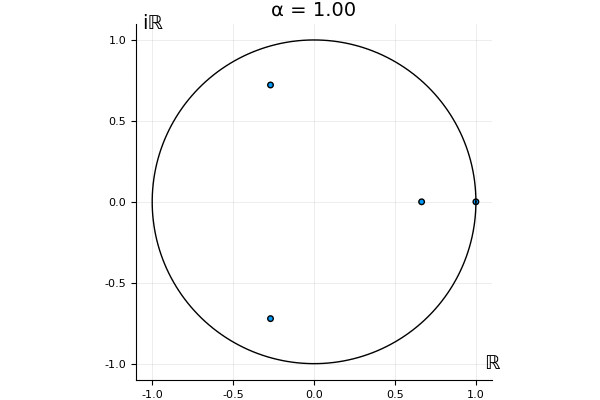
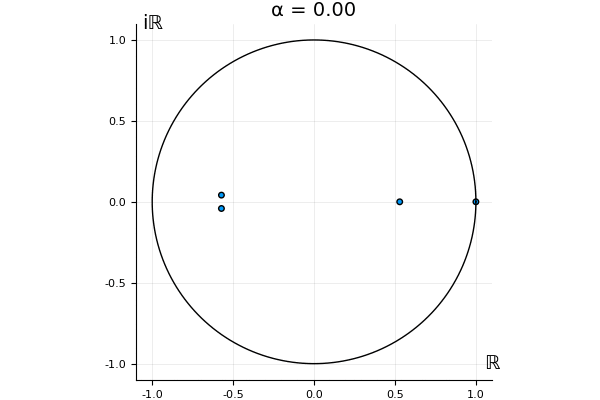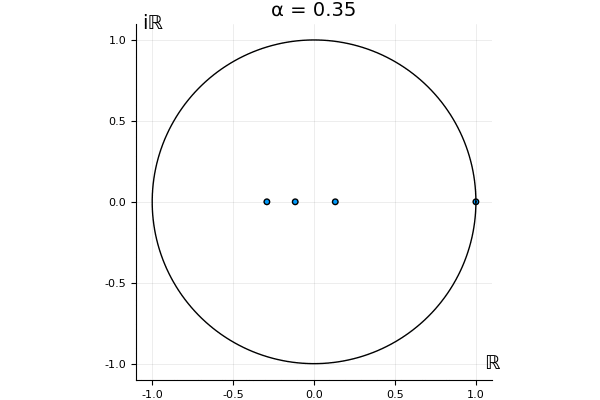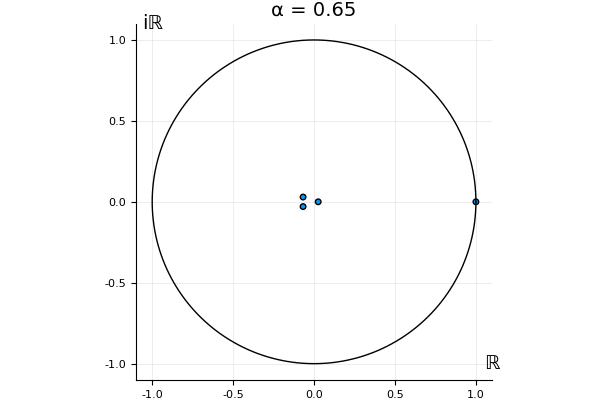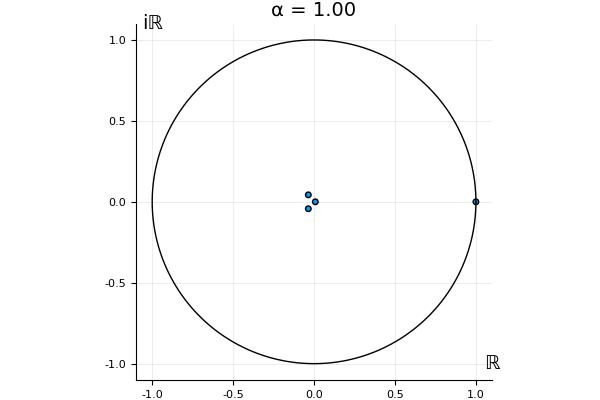
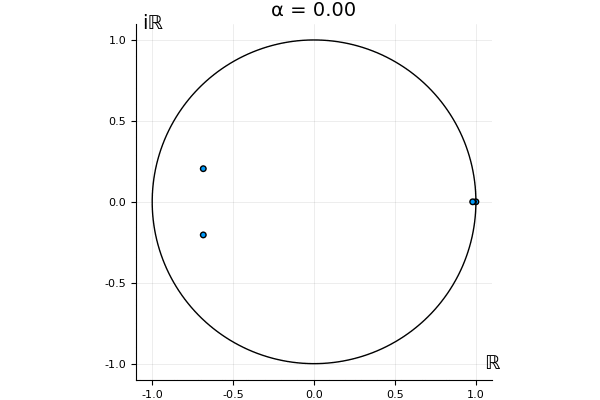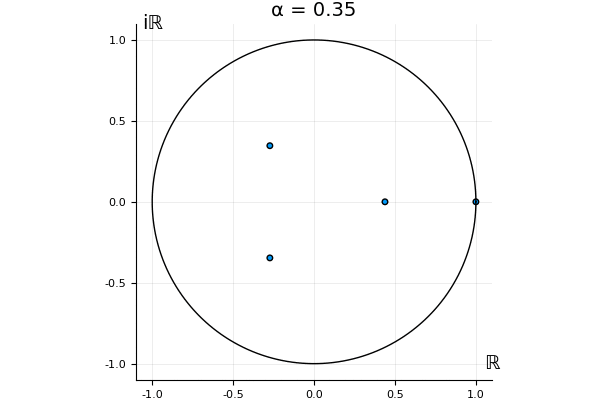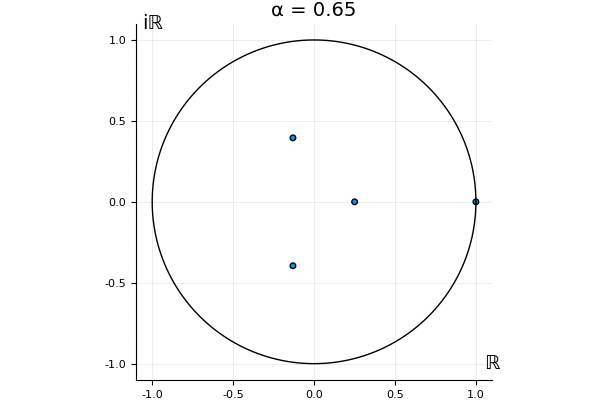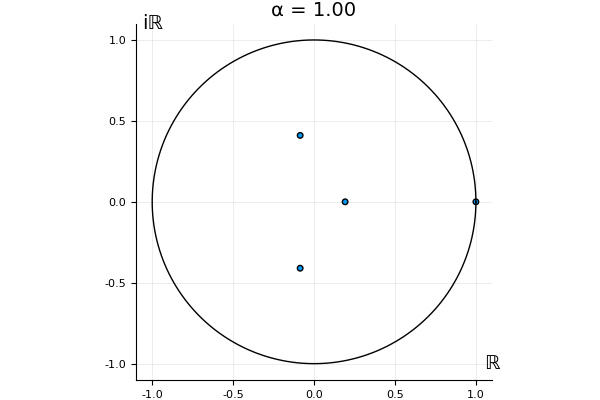
But what happens to the other eigenvalues?
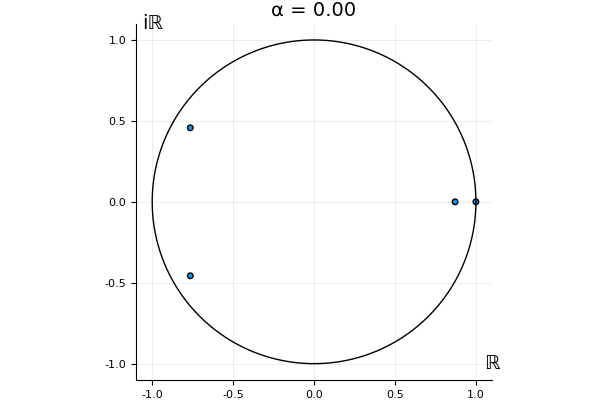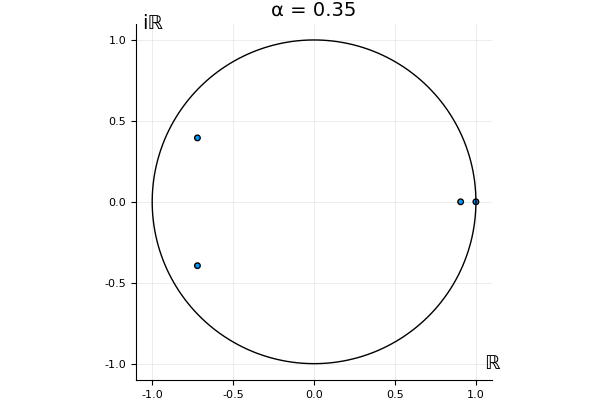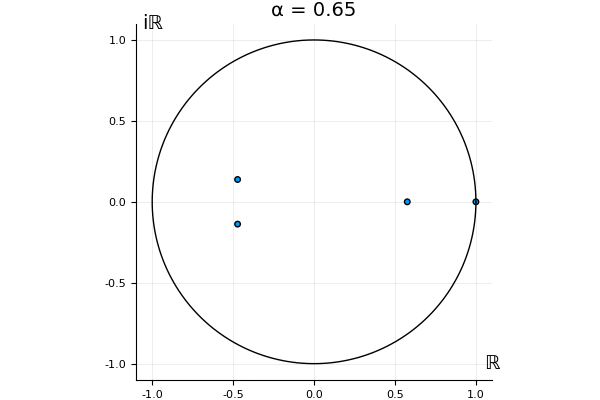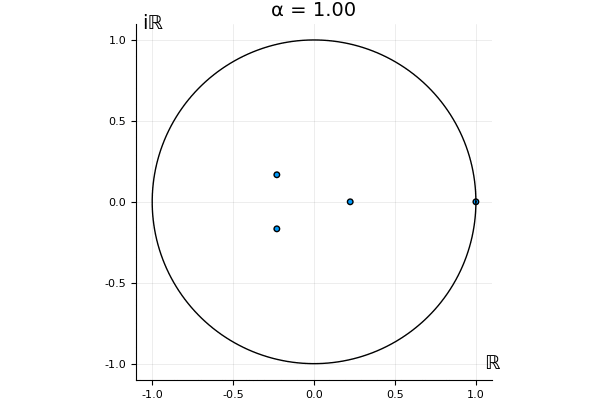
That’s the motivating question for these numerics. Maybe they don’t change either. Maybe they all shrink to zero as \(\alpha\) increases. Maybe they just rotate around in a circle. To investigate this, I randomly generated some maps \(\phi\), and looked what happened to the eigenvalues of \(\hat \phi^{(\alpha)}\) while changing \(\alpha\) in the interval \([0,1]\). And of course, the resulting animations are the gifs at the top of the post. The last two are examples of particular interest, and are not randomly generated– and nothing movesActually, shortly after I posted this I realized that in the second example, the eigenvalues do move— just very slowly, and it’s not really visible in this gif.
! But for the general (random) ones, it looks like almost anything can happen. Cool!
More information
The preprint arxiv/1705.08281 has much more motivation for why we are interested in the maps \(\phi^{(\alpha)}\) and \(\hat \phi^{(\alpha)}\). In particular, \(\phi^{(\alpha)}\) is the (Hilbert-Schmidt) adjoint of the map \(\mathcal{L}_Y^{(\alpha)}(s)\) which is featured in Proposition 3.5. The Perron-Frobenius theory of these deformed maps is investigated in Appendix A. The two examples for which none of the eigenvalues move with \(\alpha\) are Example 4.5 and Example 5.11 in the preprint.
The numerics were done in Julia, and the raw code is here. I also have it as an IJulia notebook available here. And if you just want to scroll through it, an HMTL formatted version is here.
More eigenvalues
